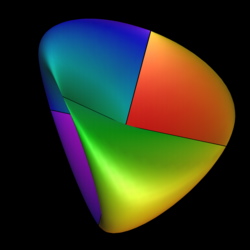
The Veronese Surface
The projection of the Veronese surface as Steiner's Roman surface.
The Veronese surface is an embedding of the real projective plane which starts with the hemisphere x2 + y2 + z2 = 1, z < 0 and maps each point (x,y,z) to 6-space. The projection of this surface (x2,y2,z2,Ö2 xy,Ö2 yz,Ö2 zx) from 6-space into 4-dimensional space given by (Ö2 xz,Ö2 yz, (1/Ö2)(x2 - y2), Ö2 xy) is again an embedding and we examine a family of projections of this surface into 3-dimensional subspaces (all of which must have local singularities). This will appear in a paper on normal Euler classes by the author.
The paper referred to was published, in expanded form, as a collaboration with Ockle Johnson [11] twenty years after the Helsinki Congress! In the meantime, several other papers of the author have used the fact that the normal Euler class of a surface embedded in four-space can be obtained as an indexed sum of singularities of any generic orthogonal projection into a hyperplane. Since the normal Euler class of an embedded real projective plane is non-zero, there must be singular points for almost any such projection.
The projection into the last three coordinates gives a cross-cap with two pinch points (Whitney umbrella points). The linear interpolation of the left hemisphere into the cross-cap is a regular homotopy right up to the last instant when opposite points on the equator are identified, forming a segment of double points.
Deforming a hemisphere into a cross-cap is a another remarkable use of linear interpolation between surfaces with the same parametrization. It is a challenge, however, to position the surfaces so that the intermediate stages are all embedded with two-fold symmetry. One way is to interpolate between the cross-cap
(1/Ö2) (sinu sin2v,cos2u(1+cos2v),sin2u(1+cos2v))
and the hemisphere given by (sinv,-sinucosv,cosu cosv) where u goes form 0 to p and v goes from -p/2 to p/2.
Rotating in the plane of the first and third coordinates gives a deformation from the cross-cap to Steiner's Roman surface (Ö2 xz,Ö2 yz, Ö2 xy) with tetrahedral symmetry. This projection has six pinch points that are the end-points of three double point segments intersecting in a triple point. These examples are described in the classical book, "Geometry and the Imagination" by Hilbert and Cohn-Vossen. The embedding in 4-space is tight (i.e. almost every height function when restricted to the surface has exactly one maximum and one minimum) and this property is shared by the images in 3-dimensional subspaces. These examples lead to the conjecture that any stable tight mapping of the real projective plane into 3-space must have either two pinch points or six pinch points.
This conjecture was established in the Ph.D. thesis of Leslie Coghlan, under the author's direction [21,22].
The paper referred to was published, in expanded form, as a collaboration with Ockle Johnson [11] twenty years after the Helsinki Congress! In the meantime, several other papers of the author have used the fact that the normal Euler class of a surface embedded in four-space can be obtained as an indexed sum of singularities of any generic orthogonal projection into a hyperplane. Since the normal Euler class of an embedded real projective plane is non-zero, there must be singular points for almost any such projection.
The projection into the last three coordinates gives a cross-cap with two pinch points (Whitney umbrella points). The linear interpolation of the left hemisphere into the cross-cap is a regular homotopy right up to the last instant when opposite points on the equator are identified, forming a segment of double points.
Deforming a hemisphere into a cross-cap is a another remarkable use of linear interpolation between surfaces with the same parametrization. It is a challenge, however, to position the surfaces so that the intermediate stages are all embedded with two-fold symmetry. One way is to interpolate between the cross-cap
(1/Ö2) (sinu sin2v,cos2u(1+cos2v),sin2u(1+cos2v))
and the hemisphere given by (sinv,-sinucosv,cosu cosv) where u goes form 0 to p and v goes from -p/2 to p/2.
Rotating in the plane of the first and third coordinates gives a deformation from the cross-cap to Steiner's Roman surface (Ö2 xz,Ö2 yz, Ö2 xy) with tetrahedral symmetry. This projection has six pinch points that are the end-points of three double point segments intersecting in a triple point. These examples are described in the classical book, "Geometry and the Imagination" by Hilbert and Cohn-Vossen. The embedding in 4-space is tight (i.e. almost every height function when restricted to the surface has exactly one maximum and one minimum) and this property is shared by the images in 3-dimensional subspaces. These examples lead to the conjecture that any stable tight mapping of the real projective plane into 3-space must have either two pinch points or six pinch points.
This conjecture was established in the Ph.D. thesis of Leslie Coghlan, under the author's direction [21,22].
The Flat Torus in the 3-Sphere